In this post I explain the way I came to reason about the Monty Hall problem and provide a tool for you to run experiements to see the outcome of different strategies for playing the game.
The Monty Hall problem is an interesting probability teaser. The premise is this: suppose you are at a game show with three doors, one of which has a prize. You, as a guest, have two chances of choosing a door to win the prize. The first time you choose, the host eliminates one of the other doors, leaving you with two. So suppose you pick door number 1, the host could then open door number 2 to show you there is nothing behind it, leaving you with 1 and 3. At this point, you get to make your second choice, choosing between 1 and 3. The question of posed in the puzzle is: do you stick with your first choice or switch?
Many folks, including myself, can assume by way of intuition that it doesn’t matter because you have a 50/50 chance of winning. However, you are actually more likely to win if you switch.
The truth is, both are technically correct. But, the intuitive answer is an answer to a different question than the one posed. We will see why that is in a minute. First, let’s clear some assumptions about the game.
Presumptuous assumptions
One of the key assumptions of the game is wether or not the host, Monty Hall, knows which door has the prize. For this exercise in thought, we will assume that is in fact the case.
Knowing this, the host will do one of two things:
(1) If you choose the door with the prize the first time, the host will eliminate one of the other doors by random chance
(2) If you choose a door without the prize, the host will eliminate the other door that doesn’t hide the prize
In either case, you will be left with two options: one with the prize and the other without. Note that in this puzzle, no matter how many doors you are given in the beginning, you are left with two to choose from in the end.
A game of chance
First of all, the way to look at the problem is this: in the beginning of the game, when you are given a choice betwen three doors, you are not aware of which of them has the prize. At this point, guessing randomly, you have a 1/3 chances of being right, i.e. 1/n for n doors. This is very important. Given n doors to choose from, one of which hides the prize, the probability of the door you pick being the one that hides the prize is 1/n, because any one of them could hide the prize, as far as you as a contestant are concerned. Therefore, the probability of one of the other doors hiding the prize, instead of the one you picked, is 1 - (1/n). Those are the chances of you being wrong in your first choice.
I: You have a 1/n chances of being right about which door has the prize behind it the first time
II: Given I, you have 1 - (1/n) chances of being wrong in your first choice.
III: The more doors you have to choose from the in beginning, the less chances you have of being right the first time you pick one.
Round II
Now, at this point, assuming Monty Hall has eliminated one of the doors that had nothing behind it (n - 2 doors for a game with n doors), you are left with two doors. One has the prize and other does not. One is the first one you picked and the other is one of the ones you didn’t pick.
The question asked is, are you better off switching or sticking to your first choice?. And the answer is rather simple: considering I, II and III, and knowing that the host is leaving you with one door that has the prize and the other that doens’t, you are better of switching. Why?
Because the chances that the other doors have the prize is 1 - 1/n, which is higher than 1/n for any n > 2. Since there is only one of those other doors left, and you know that one of the doors in front of you has the prize, that door, the one you didn’t pick the first time, has a 1 - 1/n chance of housing the prize. Your first choice, which you made when you had n options, still only has 1/n chances of being the right one, and you are still 1 - 1/n likely to have made the wrong choice.
If you have three choices in the beginning, then the chances of you being right are 1/3 while the chances of you being wrong were 2/3. Given these odds, you are before off always switching. The more doors you have to choose from in the beginning, the less likely you are to be right the first time around. For example, if there are 100 doors to start with, and you choose one, you have 1/100 (1%) chance of being right and 99/100 (99%) chance of being wrong (1 - 1/100).
IV: The higher n is in the beginning, the better off you will be if you switch in the end to the other door that is left standing.
We will make a visual observation of this in a moment, but first, let’s address the question that the intuitive 50/50 chance is actually answering.
Fair gain
The game is bit tricky because it sets up a scenario with two options, switching or maintaining, when there is in fact a third one: flipping a coin.
As a guest, you could always forget what your first choice was (or at least pretend to), and just toss a coin to choose one of the two doors that are left. In this scenario, assuming you have a fair coin, then the chances of you winning are in fact 50/50. Why?
Because in this situation, you are now facing two options of which you virtually know nothing about. It is as if you have been brought back to the beginning of the game, but instead of three or more doors you are simply given two of them. And provided that one of these has the prize and the other doesn’t, if you guess randomly you have a 50/50 chance of being right and finding the prize behind the door you choose.
V: If you choose between the two last standing doors at random, you have a 50/50 chance of winning the prize.
The figures below illustrate points I to V. The first one describes how your chances of guessing correctly the first time you choose diminish as we increase the number of doors to choose from. There are two important points to highlight. The green and the red one. The green represents the probability you have of being right when you choose, at random, between two doors, which is 50%. And the red highlights the chances of you have of choosing correctly, at random, between three doors.
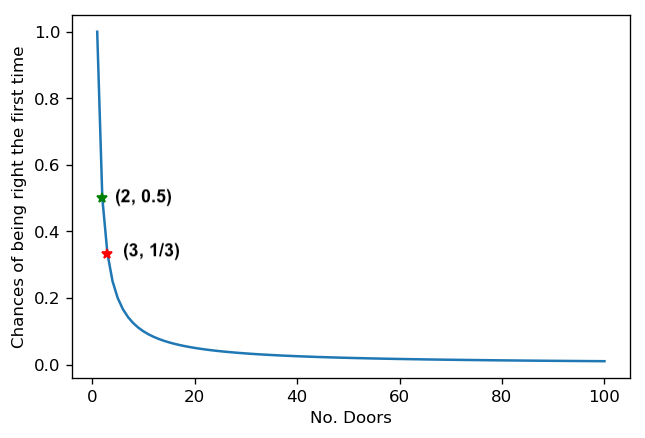
The other graph illustrates the other side of the same story: the more doors you have, the more likely you are of being wrong with your first choice. Hence, the more likely it is that the other door left standing is in fact hiding the prize.
And this leads us to our last finding about which strategy works best when making the second choice:
VI: Provided that n > 2 at start, when making the second choice: always switching > tossing a (fair) coin > always sticking to your first option.
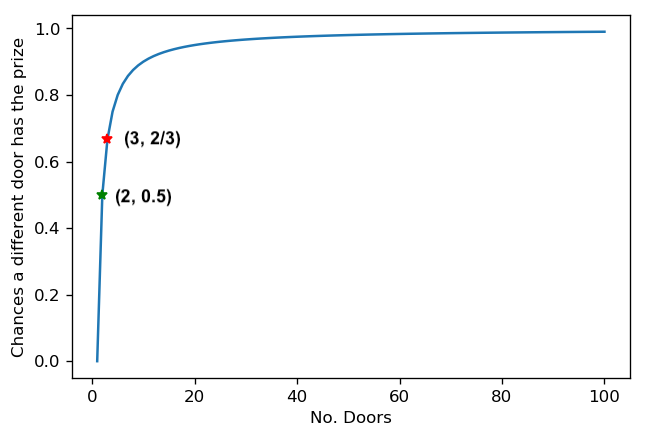
We can formally describe this by considering what happens when you choose at random on the second try:
(1) From I and II, we know that the chances of guessing correctly at first are always 1/n.
(2) We also know that the chances of the other door left standing after the others are eliminated hiding the prize is 1 - 1/n from III
(3) When we toss a coin, instead of deciding to either stick to our initial choice or switching, we even out the odds of winning and losing, i.e.:
VII: P(winning) = 1/2(1/n) + 1/2(1 - 1/n) = 1/2
This is because, by guessing at random for the second choice, we effectively get a 50% chance of ending up a 1/n chance of winning (first choice) and 50% chance of ending up with a 1 - 1/n chance of winning (the other door). This holds true regardless of how many doors there were in the beginning. You can verify this yourself by working out VII.
Experimental Verification
To see the problem in action, I created a simple game simulation program in python. You can run the simulation by giving it three parameters: the number of doors for the first choice, the number of times the game should be played, and the strategy to play with: switch, fixed or random. The code for it is as well as instructions on how to run the simulation are on Github.
The reason I wrote the simulator is because at first, it wasn’t easy for me to understand (or accept) the rationale for switching being the best alternative. Furthermore, the explanations I read from certain sites did not prove satisfactory, either because they focused on the three doors scenario or because I was biased towards my initial intuitive answer which was in fact the answer to a different question than the one posed by the problem. And so I decided I needed to explain the problem to myself, by working it out. And in the course of the writing the simulation, as I had to work through the details of what happens in the first round as well as in the second one, it became clear to me why the outcomes of switching, sticking to the first option and guessing at random are what they are, and was able to describe it in ways were more, I dare say, “intuitive” to me.
If you’re still in doubt, I encourage you to run the simulator as many times as you’d like. And if that fails to convince you, then I suggest to you write a simulator yourself and work through the details of the problem.
You can read about the history of the Monty Hall problem on Wikipedia.