In my previous post, A Fable of an Aggregator, I dedcribed the properties of an abstract data type (ADT) that enables concurrent execution of aggregations, such as sum, mean, max.
For example, if we want the mean of a collection of values, it sufficies for us to accumluate its sum and count - dividing the former by the latter gives us the answer. More importantly, this accumulation can be done concurrently - and hence, it’s parallelizable.
For some problems though, applying such techniques can be more tricky. Either because of the nature of the events or the nature of the computation. Estimating the variance of a collection of values in an online fashion is one such case. In this post, we’re going to see how we can address it.
Variance
Knowing the variance is important in many scenarios, because it gives us an idea of the spread in our data. Typically, the standard deviation is used to measure spread, as a relative measure to the mean. But the standard deviation is derived from the variance, so if we have the variance we can get the standard deviation.
The formula for the variance is straightforward: \({Var(x) = E[(X - \mu)^2]}\)
We sum up the square of the differences between each value in our collection and the mean. And this is where we meet our challenge: we need to know the mean in order to compute the difference between each value and it.
An obvious solution to this is to do a double pass on the data: first, compute the mean, and then, compute the variance. However, it is not all that uncommon for us to face scenarios in which this is hard or impossible to do. For example, we might be unable to keep the whole data (or even a sample) for legal reasons, or we might just lack the resources to do it - think of constrained platforms.
Fortunately for us, these type of problems have been thought of and solved by people before us. For the variance, in particular, there is single pass algorithm called the Welford’s online algorithm, which allows us to compute the variance in a single pass through the data.
Welford’s Online Algorithm (for Variance)
Welford’s online algorithm is an algorithm for computing the mean and estimating variance from a collection of values in a single pass, i.e. we only look at each value in the sequence once. That way, we don’t have to keep all of the values or do a double-pass. Below is a snippet of code with a python implementation.
import math
from typing import Union
import numpy as np
class OnlineStats(object):
"""
See Welford's online algorithm for variance:
https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#On-line_algorithm
Note: M2 in the formula is `_mean_sum_square_diff`
"""
def __init__(self):
self._count = 0
self._mean = 0.0
self._m2 = 0.0
def update(self, new_value: Union[int, float]) -> None:
"""
Updates the arithmetic mean (using a continuous mean formula) and the variance using Welfords's continuous formula for variance.
"""
existing_agg = (self._count, self._mean, self._m2)
self._count, self._mean, self._m2 = welford_online_variance_update(
existing_agg, new_value
)
def mean(self) -> float:
return self._mean
def sample_variance(self) -> float:
return float("nan") if self._count < 2 else self._m2 / (self._count - 1)
def variance(self) -> float:
return float("nan") if self._count < 2 else self._m2 / self._count
def sample_std(self) -> float:
return math.sqrt(self.sample_variance())
def std(self) -> float:
return math.sqrt(self.variance())
def sample_size(self) -> int:
return self._count
@property
def m2(self):
return self._m2
def welford_online_variance_update(
existing_agg: Tuple[int, float, float], new_value: Union[int, float]
):
(count, mean, m2) = existing_agg
new_count = count + 1
delta = new_value - mean
new_mean = mean + delta / new_count
delta2 = new_value - new_mean
new_m2 = m2 + delta * delta2
return new_count, new_mean, new_m2
A favorable property of the algorithm is that we only need to keep track of three values: count, mean and M2. The algorithm relies of recurrence - which means that every new value will depend on the previous one.
With this algorithm, we can estimate the mean and variance, looking at one value at a time. Our storage and memory requirements become much less of a burden.
While this is great, when our dataset is large, we may face a bottleneck: we can only update the mean and variance one value at a time. This is not parallel friendly. Likewise, we may have cases where only parts of our data are available to different computing units (e.g. machines). For both scenarios, it would be great if we could use this formula concurrently. As it turns it, this is viable to do.
Chan’s et al. Parallel Algorithm
As explained in their paper, Updating Formulae and a Pairwise Algorithm for Computing Sample Variances, Chan et. al provided a method to estimate statistics from samples by relying on subsampling.
Given a sample of values \(n\), they propose dividing it into subsamples of \([1, m]\) and \([m+1, n]\) values.
For each subsample, we can compute the variance using any formula - in our case, we can use the Welford’s algorithm for a single pass computation - and then, the results can be combined with a general formula:
$$Var_{1,m+n} = Var_{1,m} + Var_{m+1,n} + \frac{m}{n(m + n)} *(\frac{m+n}{m}T_{1,m} - T_{1,n+m})^2$$
Where \(T\) is the sum of the samples. They propose that the data can be subdivided into as many subsamples as we’d like: which means we can parallelize our computations as much as possible. However, the authors further argue, and demonstrate empirically, using subsamples of sizes \(m> 1\) yields more accurate estimates of the variance compared to the the two-pass method, and more stable results than using \(m = 1\). What that means is that we should avoid using Welford’s algorithm on single samples - this is in fact impossible, single Welford’s variance is only defined when \(m > 1\).
With Welfords’ algorithm, we accumulate the count, mean, and M2 values for each subsample. Thus, the way to combine them is as follows:
def combine_online_stats(rss_a: OnlineStats, rss_b: OnlineStats) -> OnlineStats:
"""
Combines running sample stats instances using Chan et al.' algorithm.
"""
count = rss_a.sample_size() + rss_b.sample_size()
delta = rss_b.mean() - rss_a.mean()
mean = rss_a.mean() + delta * rss_b.sample_size() / count
m2 = (
rss_a.m2
+ rss_b.m2
+ (delta * delta) * ((rss_a.sample_size() / rss_b.sample_size()) / count)
)
return OnlineStats.create(count, mean, m2)
Alternatively, we can use the estimated variance from each subsample directly, provided that we’re keeping track of the sum of samples - based on the formula from earlier.
And with that, we can make use of Aggregators to compute the variance in an online fashion. Let’s compare the results from using this approach against the two-pass method. We’ll make use of numpy’s implementation of mean and variance for comparison.
Comparing Results
To observe the reliablity of the results empirically, we run a simulation with two distributions: (1) standard normal and (2) binomial. In both cases, we generate samples of different sizes: 100, 1000, and 10000. For each sample size, 1000 arrays are created with elements drawn from distributions of random parameters, and we plot the change for the mean and variance from the two-pass approach, i.e. for each sample (of each size), we computed and mean using the online approach and then two-pass approach, and then we compute the normalized delta of the former relative to the latter. The plots depict, essentially, how far from the two-pass approach the mean and variance were — in terms of percentage points.
It’s also worth noting that for the online variance approach, the samples of values were broken into a random number of sub-samples (two to 10) of almost equal sizes to simulate merging results.
Standard Normal Distribution
For samples drawn from standard normal distributions, the following can be observed:
- The estimate of the mean with the online approach has a very small delta range — notice the scale of the x-axis.
- The variance, on the other hand, has relatively large delta ranges.
- For samples sizes of 100, the extreme cases are around 30%, and majority is below 10%.
- The delta range reduces by the same order (of magnitude) as the sample size increases - with 1000 samples, the delta range is 2.5% and with 10000 points it’s 0.25% in the extreme cases.
- Interestingly, the variance estimated with the online method is consistently higher than the value obtained with the two-pass approach.
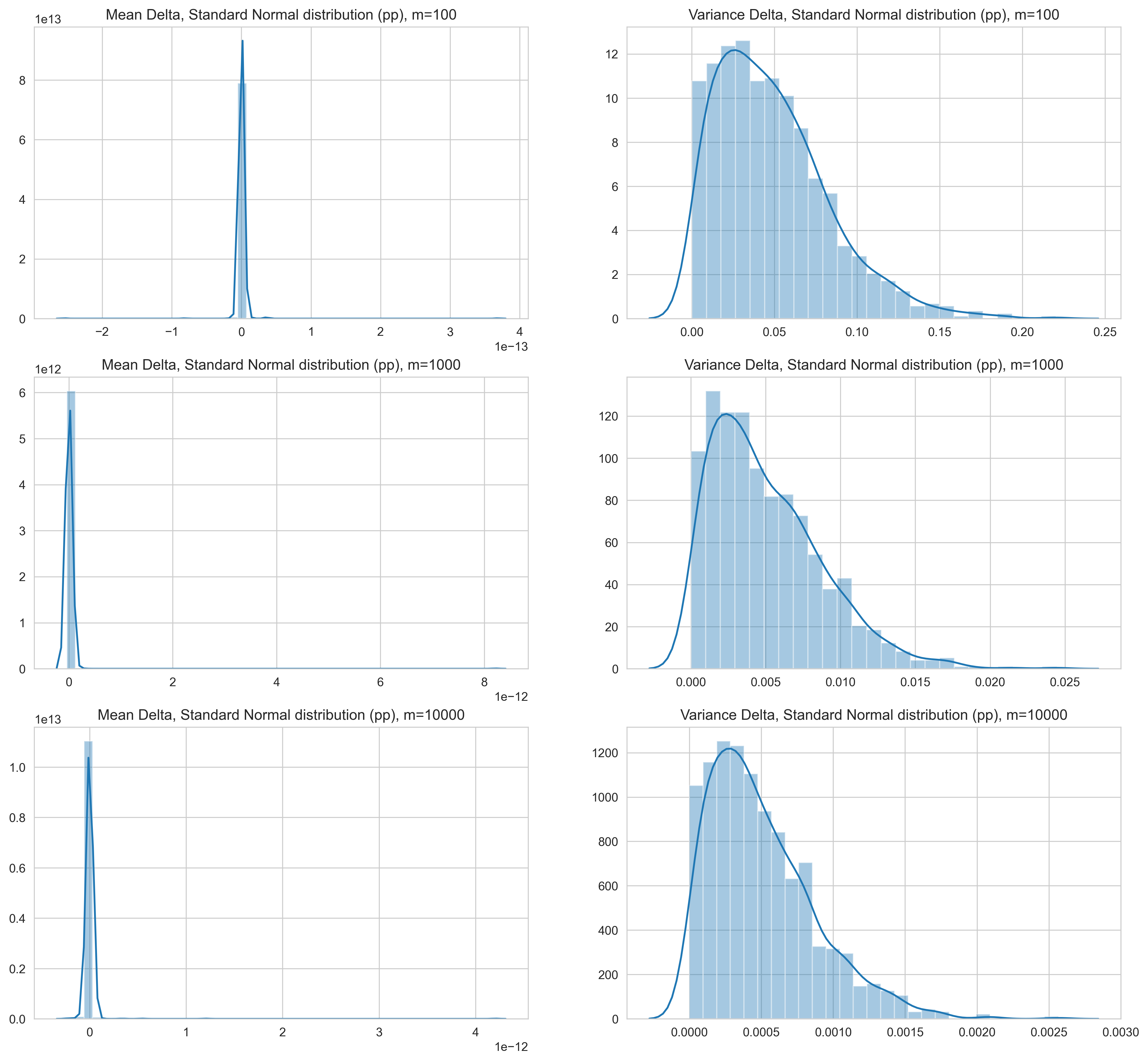
Figure 1: Normalized delta (change) for mean and variance between the online approach and two-pass approach for standard normal distribution samples. Values are in percentage points.
Binomial Distribution
For samples drawn from binomial distributions, we make similar observations
- The estimate of the mean with the online approach has a very small delta range and the delta is highest with 100 samples (smallest sample size).
- What stands out is the more normal distribution shape of the delta of the mean.
- The variance follows a similar pattern of decrease in delta following the increase in order of number of samples.
- As with the standard normal distribution, the variance estimated with the online method is consistently higher than the value obtained with the two-pass approach.
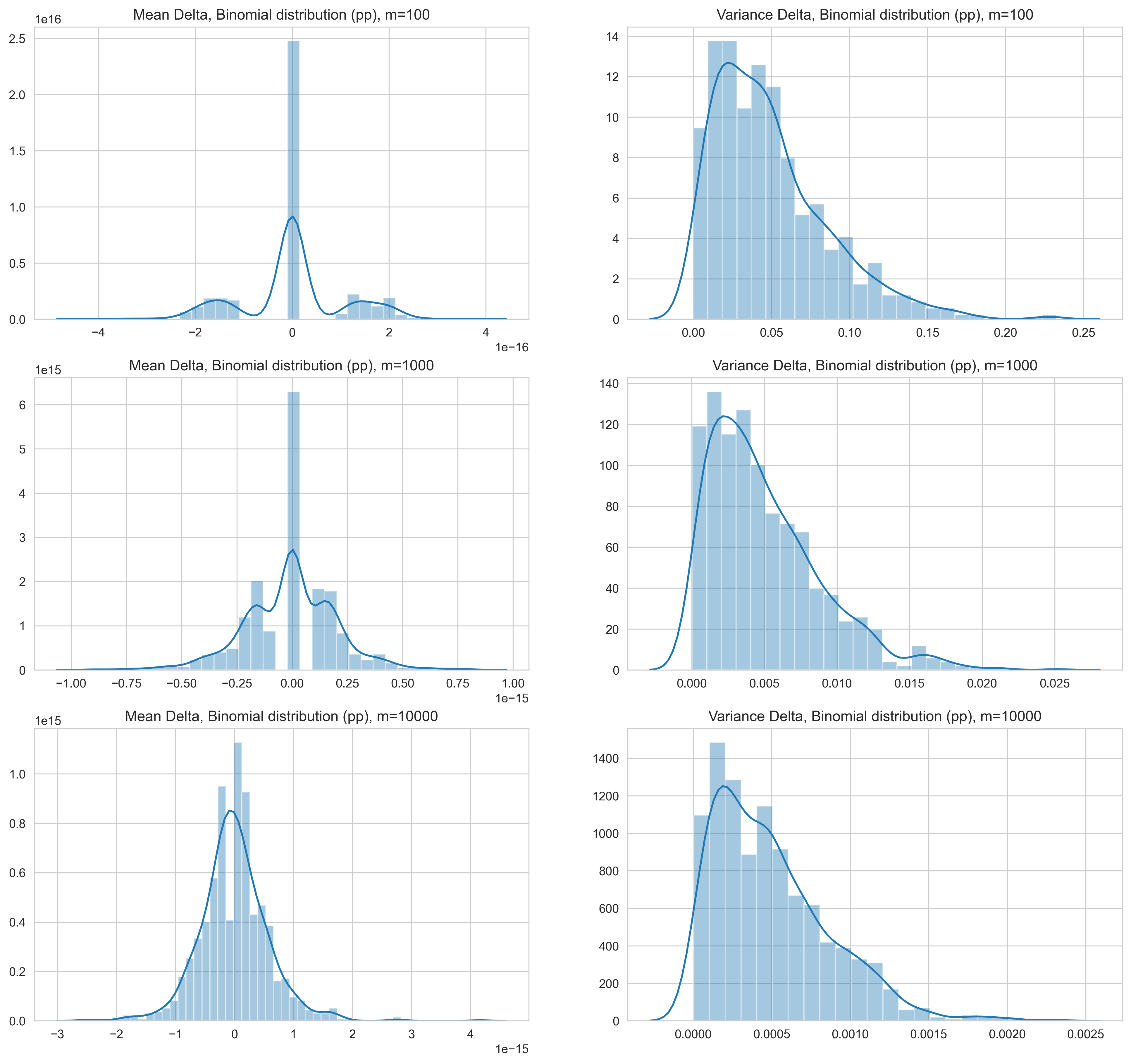
Figure 2: Normalized delta (change) for mean and variance between the online approach and two-pass approach for binomial distribution samples. Values are in percentage points.
With these results, we can derive the following for using Welford and Chan et al’s method for online variance: use at least 1000 values for single digit delta ranges and 10000 for less than 1% delta compared to the two-pass approach - in the extreme cases.
The accompanying notebook for this post is on github.
Conclusion
We set out to experiment with an approach to estimate the variance in an online fashion - i.e. by doing a single pass through the data, saving up on storage and/or compute. We explored Welford’s algorithm for estimating the variance that way, and Chan et al’s approach for combining the estimates from different sub-samples so we could enable concurrent estimation of the variance. With both methods together, we can estimate the mean as well. To understand their behavior better, we simulated their usage on many samples from two distributions - standard normal and binomial - and found the delta for the variance to be larger than the mean and inversely proportional to the magnitude of the sample size.
There are similar algorithms created for other statistics and data mining estimates out there. They can be interesting to explore for cases where resources are constrained or we just need a more efficient way to estimate our statistics over large sets of data in a concurrent fashion - as long as we understand the trade-offs we’re making.